Flatten a Nested List

Overview

The objective of this problem is to design an Iterator that can efficiently flatten a nested list, so that users can use the Iterator to iterate over each element within the original list.

Problem Statement

We are given a List of elements - nestedList. Each element within this list is either an integer or a list whose elements can in turn be integers or another list. Implement an iterator to flatten the input nestedList.

Formally, we have to implement the NestedIterator class such that:
- NestedIterator(List<NestedInteger> nestedList) initializes the iterator instance with the nested list: nestedList.
- int next() returns the next integer in the nested list.
- boolean hasNext() returns True if there are still some elements in the nested list and False otherwise.

The pseudo-code for testing the solution is as follows:
result = []
while iterator.hasNext()
    append iterator.next() to result
return result

Please try to solve the problem before looking at the solution below and share your thoughts in the comments section below.

Solution

My initial thought was that the flattening logic needs to be done recursively until you find an integer or run out of elements in the current list being processed. It is not quite intuitive, at least wasn’t for me, that the hasNext() fn. needs to contain the logic that tells whether the current element is returnable i.e. an integer or not. Think of hasNext() as the brain of the iterator instance, that knows when to return the required element to its caller.

To keep things simple, I decided to use a stack data-structure to emulate processing of elements in the nestedList recursively. Initially the entire input nestedList would be pushed to the stack as the current element being processed.

The idea behind using a stack is that while processing the current list, if you encounter another nested list – B within the current list A, you would have to complete the processing (flattening) of this nested list B before moving on to the next element in A. Once, all the elements of the nestedList, stored at the top of the stack is processed, we can pop that element from the stack. Also, it is worth noting that there is no need to push a primitive integer element on to the stack.

Code

# """
# This is the interface that allows for creating nested lists.
# """
class NestedInteger:
   def isInteger(self) -> bool:
       """
       @return True if this NestedInteger holds a single integer, rather than a nested list.
       """

   def getInteger(self) -> int:
       """
       @return the single integer that this NestedInteger holds, if it holds a single integer
       Return None if this NestedInteger holds a nested list
       """

   def getList(self) -> [NestedInteger]:
       """
       @return the nested list that this NestedInteger holds, if it holds a nested list
       Return None if this NestedInteger holds a single integer
       """

class NestedIterator:
    def __init__(self, nestedList: [NestedInteger]):   # input is a List of NestedInteger objects as defined in the interface above.
        self.stack = [[nestedList, 0]]
    
    def next(self):
        top, index = self.stack[-1]
        self.stack[-1][1] +=1
        return top[index].getInteger()
 
    def hasNext(self) -> bool:
        s = self.stack
        while s:        # Loop until I find an integer or the stack is empty
            elem, index = s[-1]
            if index == len(elem):
                s.pop()
            else:
                curr = elem[index]
                if curr.isInteger():
                    return True
                s[-1][1] +=1
                s.append([curr.getList(), 0])   #only push to the stack if the curr. element is a List[NestedInteger]
        
        return False

Sample Test cases

Input: [0, 1, 1, 2, 3, 5, 8, 13, 21]
Output: [0, 1, 1, 2, 3, 5, 8, 13, 21]

Input: [1,[3,[7]]]
Output: [1, 3, 7]

Input: [1,[3, 5],[7, [19, 21, [20, 18, 0]]]]
Output: [1, 3, 5, 7, 19, 21, 20, 18, 0]

Analysis

Let’s assume that the maximum elements that each nested list can hold is N. Each element of the list can recursively grow to hold another nested list, having a maximum of N elements itself. The recursion tree can grow up to a maximum height of ‘N’ levels as shown below.

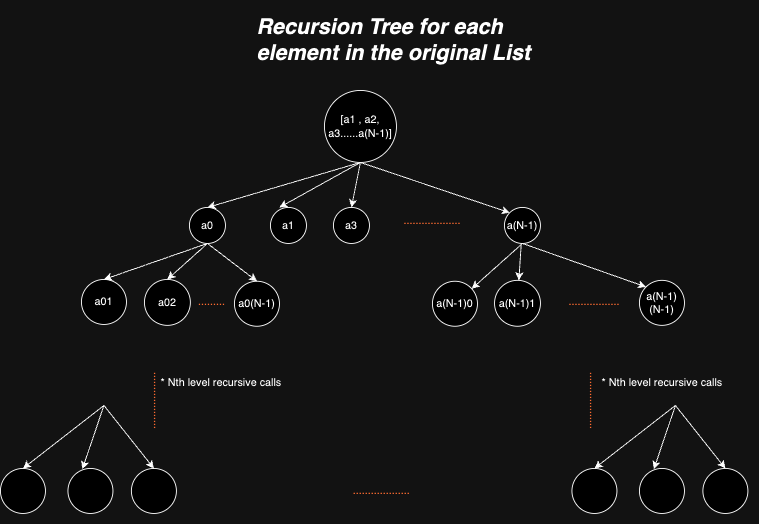
The total work done by hasNext() can be defined as the sum of work done for each recursive call since the work done in each recursive call is constant time. If we limit the level of nesting to say some constant ‘M’, then the above tree forms a finite geometric series where a = 1, r = N (common ratio between successive elements), as follows:

1 + N + N2 + N3 + N4 + ............. N(M-1)

The sum formula of a finite geometric series: a + ar + ar² + ar³ + … + a r^n-1 is

Sum of n terms = a (rⁿ – 1) / (r – 1)

In our case we get the Total sum as (N^M – 1) / (N – 1). Hence the time complexity of hasNext() fn. is

O((N^M – 1) / (N – 1)) = O(N^M)

Reference

Credit goes to user – StefanPochmann in LeetCode for coming up with this elegant and awesome solution.